
Old-school method for calculating linear ratios such as board footage. This particular example is from “Deane’s Doctrine of Naval Architecture” published in 1670. See the store page to download a free PDF that explains the process.
]]>
Old-school method for calculating linear ratios such as board footage. This particular example is from “Deane’s Doctrine of Naval Architecture” published in 1670. See the store page to download a free PDF that explains the process.
]]>
On a practical level, builders used geometry to determine if something is true. In other words, is that wall plumb, is that foundation level etc. That’s a far cry from today, where everything is described with numbers from your shoe size to the calories on that bag of chips you shouldn’t be eating.
Our new book “Euclid’s Door”, describes how to build a kit of layout tools and in the process unlock the hidden geometry. Early on, we were curious to explore just how true we could make these tools using hand methods and the power of geometry. I confess, I reached into my machinist tools to quantify the results of our efforts. That became a big “aha” moment. We discovered we could indeed make wooden tools that stand up well and even exceed their modern metal cousins. How could this be possible?
Here’s a simple but important principle. If you magnify the distance of the thing you are trying to measure, it increases your ability to gauge with precision. Using winding sticks is a good example of this in action.
The length of the sticks exaggerate the width of the board to magnify any twist. Another example is to draw two parallel lines. You can prove they are indeed parallel if you extend the lines out and they never cross. For our purposes on the tool builds we found we could achieve magnificent results extending lines out with our three foot long wooden straight edge. We used this principle to work out a simple proof for every tool.
Here’s a couple of other examples of that principle that illustrates the power of it. Take a machinist’s micrometer. It’s really just a screw that has a scale we can read to help us measure with precision. Yet it is able to perform at a high level because it mechanically exaggerates the distance of what it’s measuring. One turn of the thimble (the part that has the scale on it) advances the plunger (the part that touches the work) 0.025”. It takes forty revolutions to advance the plunger one inch.

Yet in those forty turns, the thimble travels round and round the barrel of the micrometer and in reality it travels a distance of about six inches. So the travel ratio is about 6:1. Another good example is a tall case clock. It uses weights to drive the hands, but the precision is controlled by the motion of a pendulum. In one hour, the tip of the minute hand on a dial traces a circle that’s a bit over 30 inches in circumference. In that same hour the pendulum below swings out the beat of 3,600 seconds.

In that same space of one hour, that pendulum travels over half a mile. Most clocks have a screw mechanism to raise or lower the pendulum bob. In this way, the pendulum swing can be altered slightly. This allows the clock to be adjusted with great precision.
Humor me and let me take you down a rabbit hole. Most of the things we typically measure are expressed with a number i.e. inches, pounds, minutes, etc. These measurements that are expressed as a number all require a “master” or standard. In my former life in industry we kept and maintained masters that we used to make sure the tools and product were correct. These masters were all checked ultimately against a set of “Grand Masters’ in a vault. Those Grand Masters were sent to the Bureau of Standards in Washington D.C. once a year to verify they were correct.

Not sure what the technology is today, but even back in the 1970’s, the D. C. lab checked our Grand masters against a beam of light with a wavelength that defined ground zero. In the case of measuring time, early clock makers had to turn to the heavens for a suitable time master. Note, they were looking to something at great distances to get their master time. Every major seaport across the globe went to great expense to set up and maintain a master clock that naval navigators could set their timepieces to. In both these cases the process of developing and improving a master to support the entire enterprise required tremendous resources.
Compare that to this simple geometry our ancestors discovered. It doesn’t use numbers to measure but instead uses lines to verify if something is true i.e. are the lines parallel or do they intersect in the right spot. It put tremendous power into the hands of ancient builders that only required a few bits of string and a couple of straight sticks (which are self proving). Put that in your pipe and smoke it.
]]>But back to aliens. She was convinced that the pyramids could only have been built by someone with superpowers from outer space. In her defense, she was right about something. The ancient builders who designed and executed those amazing structures did have superpowers. They mastered the power of geometry. Ironically, those ancient geometers also thought that this knowledge fell from the heavens. They might not have used those exact words but they did consider it a great mystery. Then as now, no one fully understands the mystery of geometry. At least no one knows exactly how our ancestors came to comprehend it and master it. Yet it became, and still is the foundation of the building arts.
Jim Tolpin and I have been exploring what we call “Artisan Geometry” for the last ten years. Along the way we noted something odd when we looked inside old historic tool chests. You could take all the tools and divide them into two groups. One group, like saws or chisels, were mostly acquired from specialty tool makers. A second group like squares and straight edges were often user made. This second group piqued our curiosity. They’re mostly used for design and layout and all have a strong link to artisan geometry. So we jumped down the rabbit hole and built our own kit of tools. We built several different versions of these tools and unpacked the geometry inside each one.

Besides being astounded at how functional and accurate the tools are, we came to see that each build offered a concrete hands on lesson in geometry. We think that building these tools was a door into the mysteries of artisan geometry. An important passage to cross through if you are a builder.
Euclid’s Door is now available for sale from Lost Art Press or you can purchase a copy from our website. It’s one sure way to rev up your superpowers.
George R. Walker
]]>
Or that you could use the power of a right angle to make patterns to construct complex curves? Angels (and woodworkers) may fear to tread into the land of complex shapes and curves, but armed with some knowledge of geometry and a square, you can step outside of your comfort zone.
Jim Tolpin has just completed a digital workbook titled Sections and Projections. It teaches you how to unpack and draw complex forms and curves to generate working drawings to put flesh on your ideas. He walks you through the geometry behind a progression of forms. Each new form adds a twist that expands a whole new range of creative possibilities. Not only will you understand the underlying geometry but you’ll understand how to change and adapt it to your design needs. The material is dense but made understandable by the excellent drawings of Keith Mitchell from Shipwrightskills.
If you are serious about taking your designs to a new place, check out Sections and Projections. Note, you can download the Forward and Introduction for free to get a taste for what’s inside along with a set of templates to construct some paper models of complex forms.
George Walker
2022
]]>
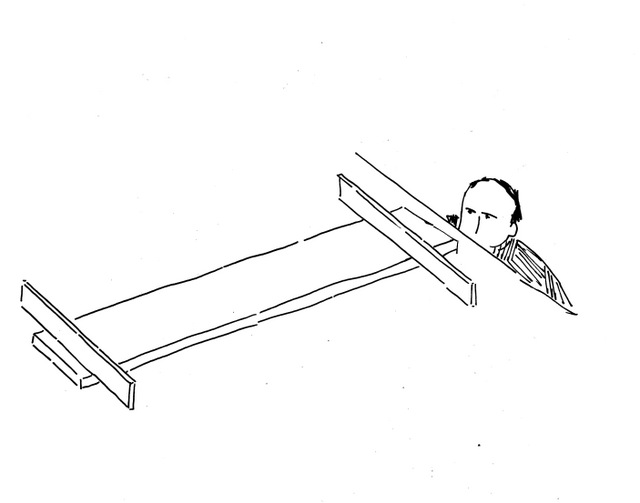
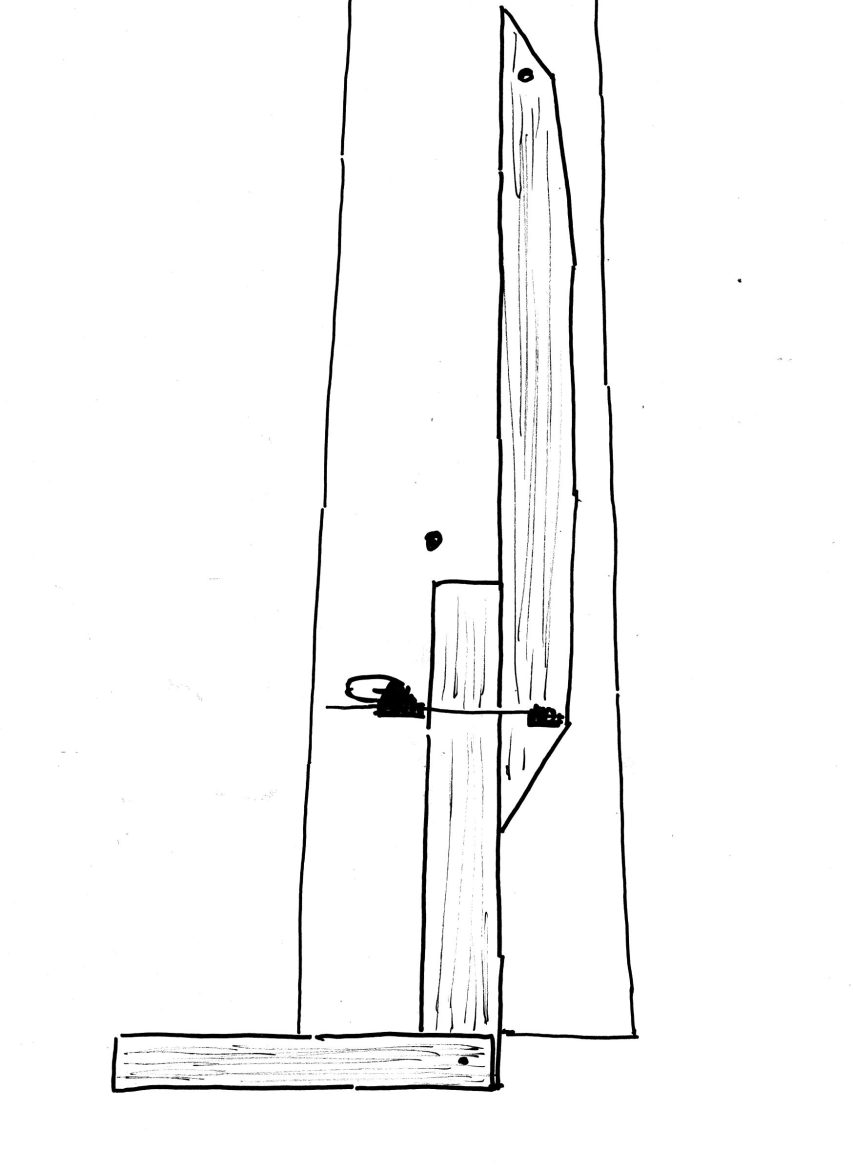
The smaller pair is a bit more mysterious. There’s a punch mark in the center of the fulcrum and the distance from the mark and the end of the legs is 16&1/2″. What’s that about? That’s actually a very important measurement to a pre-industrial artisan. That distance is exactly 1/12 of a “Rod”. A rod, also known as a perch or a pole was a standard distance used to step off longer distances before the invention of tape measures. A rod is 16 feet 6 inches long. Although that seems like an odd module to use as a standard, a 16&1/2 foot rod multiplied produced spans that were common on buildings from barns to cathedrals. For example, two rods equals 33 feet. Simple fractions of a rod like 2/3 of a rod is 11 feet. Using whole rods and simple fractions, you can step off the following distances – 11, 22, 33, 44, 55, 66, 77, 88, and 99 feet. All of these distances show up routinely in historic building foundations. Thus the divider above could be used along with a rod to step off a distance quickly and accurately. 55 feet is 3 rods plus 1/3 or four steps using our built in divider reference.
I had a few folks request more details on this particular tool, Here are some close ups

Note the grain of the wrought iron. I also wonder if the circles around the center are some sort of small scale reference or just some decoration. Any guesses how the maker would have made these rings? Yes, I know they look like they are made with another pair of dividers, but this is metal, not butter.


I’m not a smith but to my eye it looks like the legs start out square in cross section and are then forged into a tapered triangle shape except the section where the locking screw is located.




A couple of other thoughts. How much skill is required at the anvil to get these two tapered legs exactly the correct length? Along with all the other things that have to come together. From my perspective, this is much more sophisticated than it might appear. What stories could this tool tell? Who used it? What buildings did it leave it’s mark? More questions than answers.
George Walker
]]>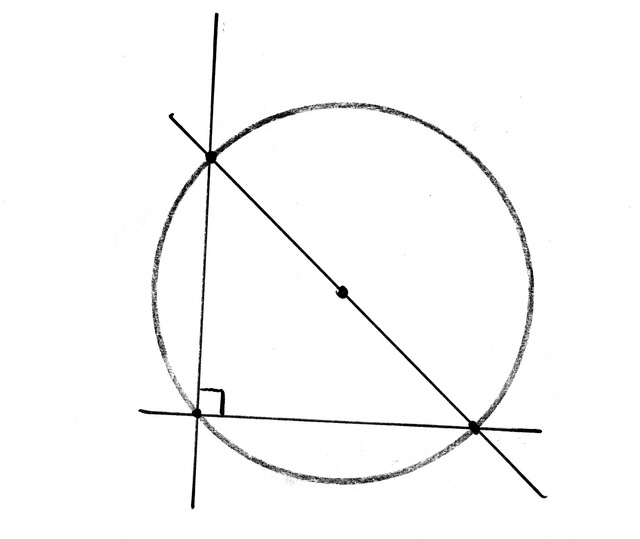
Part of this knowledge is technical. Learning to use a hand plane and shooting board to dial in the parts to a high level of perfection. The other part is more mysterious. How to use geometry to create each tool out of thin air using just a compass and a straight edge. Note – our first build is a straight edge that we use to boot strap every other tool into existence.
Euclid’s Door is a mini apprenticeship to hone you skills. Plus you end up with a killer set of of layout tools. One thought that kept dogging me as I walked through the builds. Why didn’t I learn this years ago?

We don’t have a solid release date yet due to supply chain issues, but you can sign up to be notified once it’s available at Lost Art Press.
George R. Walker
]]>
Why I Create Caravans
The first answer that comes to mind, which is probably the one closest to the truth, is the opposite of what mountaineers say when asked why they climb a mountain: “Because it’s there”. In my case, I’ve always wanted to build gypsy caravans because they are not there! (At least nowhere near me). I have long been fascinated with the traveling lifestyle, with life lived mostly outdoors, lived close to the edge—A life I lived for a decade or so in my youth. I learned that if you could live such a life in company with a cozy and enchanting conveyance in the form of a highly developed folk craft, then so much the better.
An encampment of gypsies with caravans by Vincent Van Gogh
For me, that conveyance was the English or Irish gypsy caravan (“Vardo” in the Romany language) as observed and painted by Van Gogh. Ever since having first seen this painting, and later highly romanticized illustrations of them in children’s books (see “Wind in the Willows” for starters) I began finding murky black and white photos of them taken at the end of the 19th century. I finally got my hands on a clutch of glorious color photos of restored versions at Appleby Faire in England as well as some highly detailed drawings by John Thomson. At that point I knew I had to have one. I also knew that the only way I would ever get my hands on one would be to build one.
Starting in the late 1970’s I built, and traveled in, a very simple version affixed to the frame of a 1940 Ford 1-ton pickup.
After moving to the Northwest, I embarked on building more authentically designed and detailed vardos, such as this hardtop version pictured above.
My last caravan was the “Trillium” completed in 2007. This wagon closely reproduced the look of a “bow top” style caravan that was produced by Bill Wright’s carriage shop in Leeds, England in the late 19th century.
Like most of my other wagons, I built the Trillium in collaboration with several other artists: a metal worker for the welded steel frame and some of the decorative brackets; a graphic artist for the panel art and lining out; and a stained glass maker for the windows. The current owner provided much of the fabric work of the interior decor.
The materials throughout this and all my other wagons (since my first) are marine grade. In general I used Honduras mahogany for the framework (mostly pinned tenon and bridle joints); Port Orford cedar for the tongue and groove siding; Sitka spruce for roof framing; Egyptian canvas sailcloth for the cover; marine grade oil enamel paints and bedding compounds; bronze and stainless steel fasteners and copper rove and rivets. Joinery throughout, including the interior fittings, were built to traditional joiner’s standards. That is, all the joints are mechanically interlocked and therefore don’t rely on glue or fasteners to bear loads.
None of my wagons were designed to be horse-drawn. I don’t know horses, and I don’t know how I would convince the beast to pull my wagon around the highways and byways of America. But I do know how to pull trailers behind my pickup truck, so I built my wagons to be roadworthy at highway speeds.
Of course, one can use far less expensive materials and still create a lovely caravan–it just will require more conscientious maintenance and even then may not enjoy a lifetime of use.
Whether traveling four or four hundred miles a day these wagons are the conveyances of dreams-come-true. They are a folk-craft of the hand that takes the heart home.
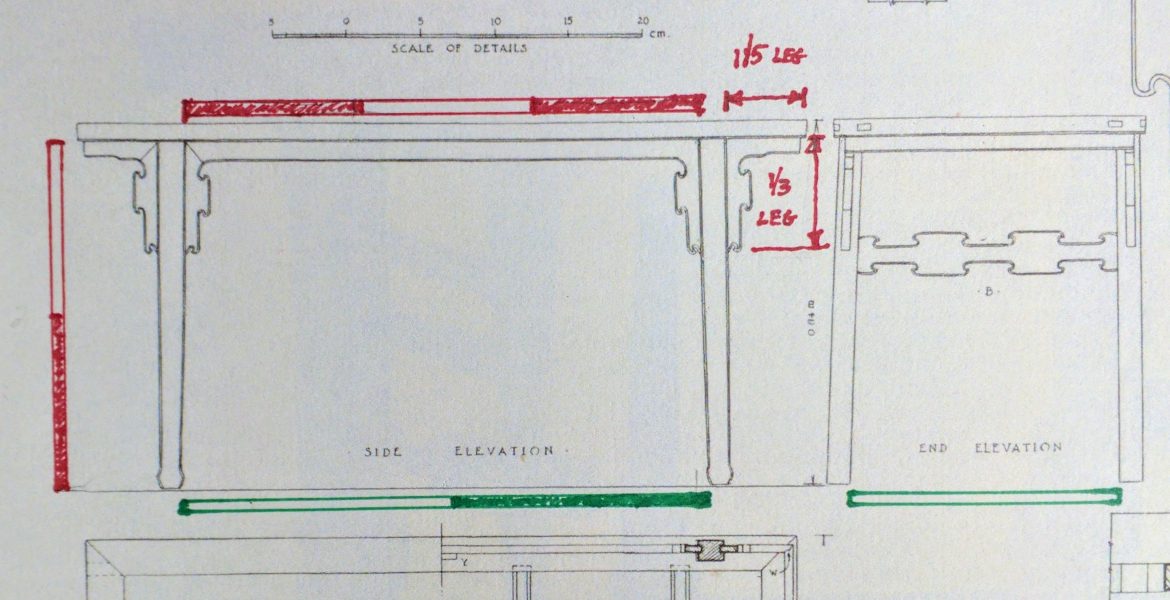
A height-to-length ratio of 2:3
A depth-to-length ratio of 1:2
An overhang of top-to-leg length of 1:5
A corbel height-to-leg length of 1:3
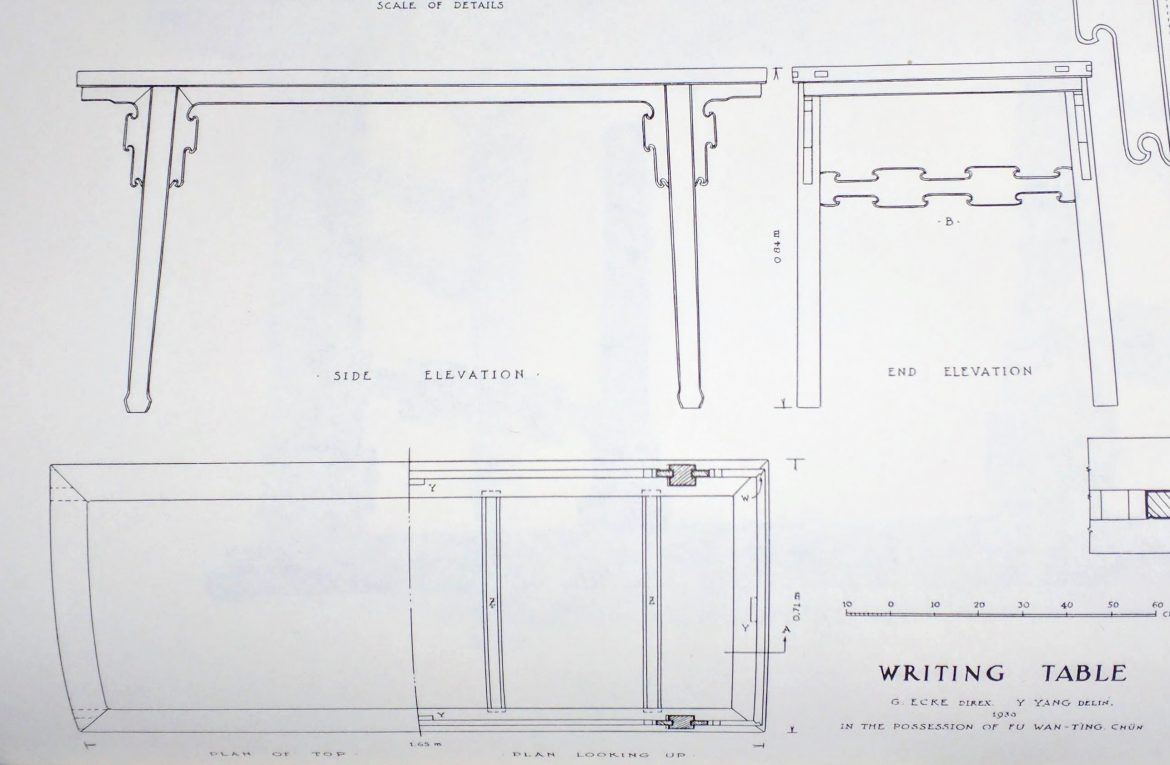
Now let’s take the dividers to another Chinese furniture piece:

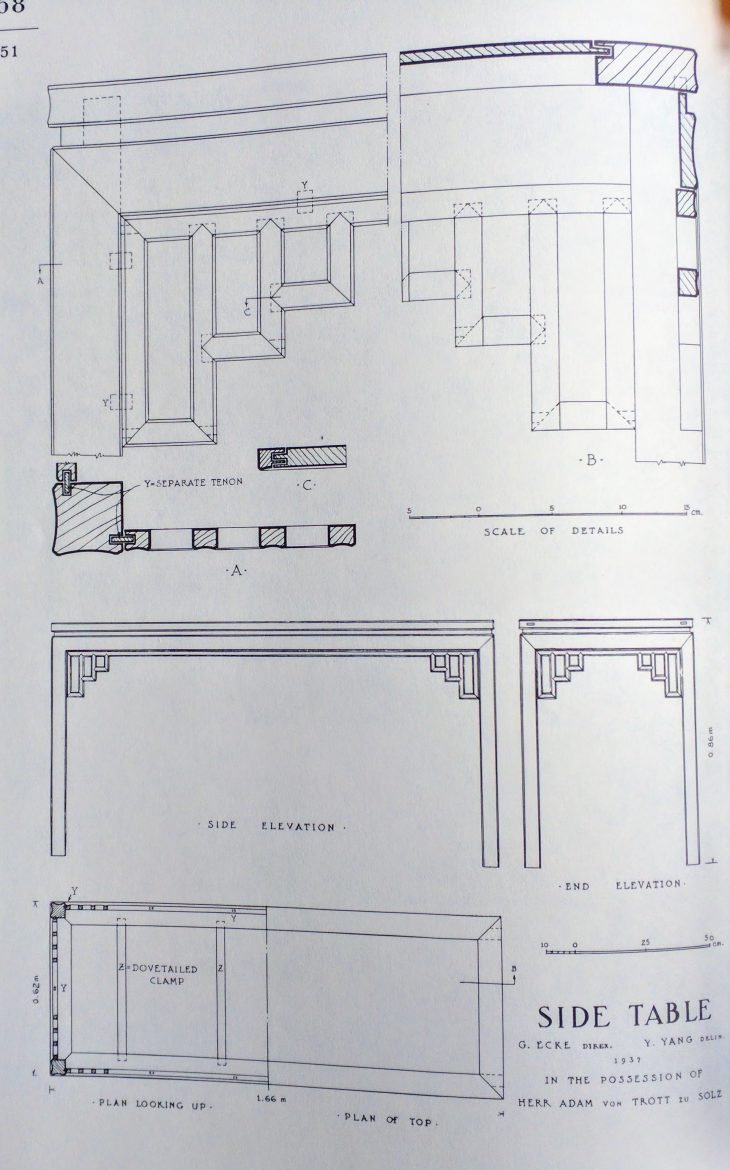
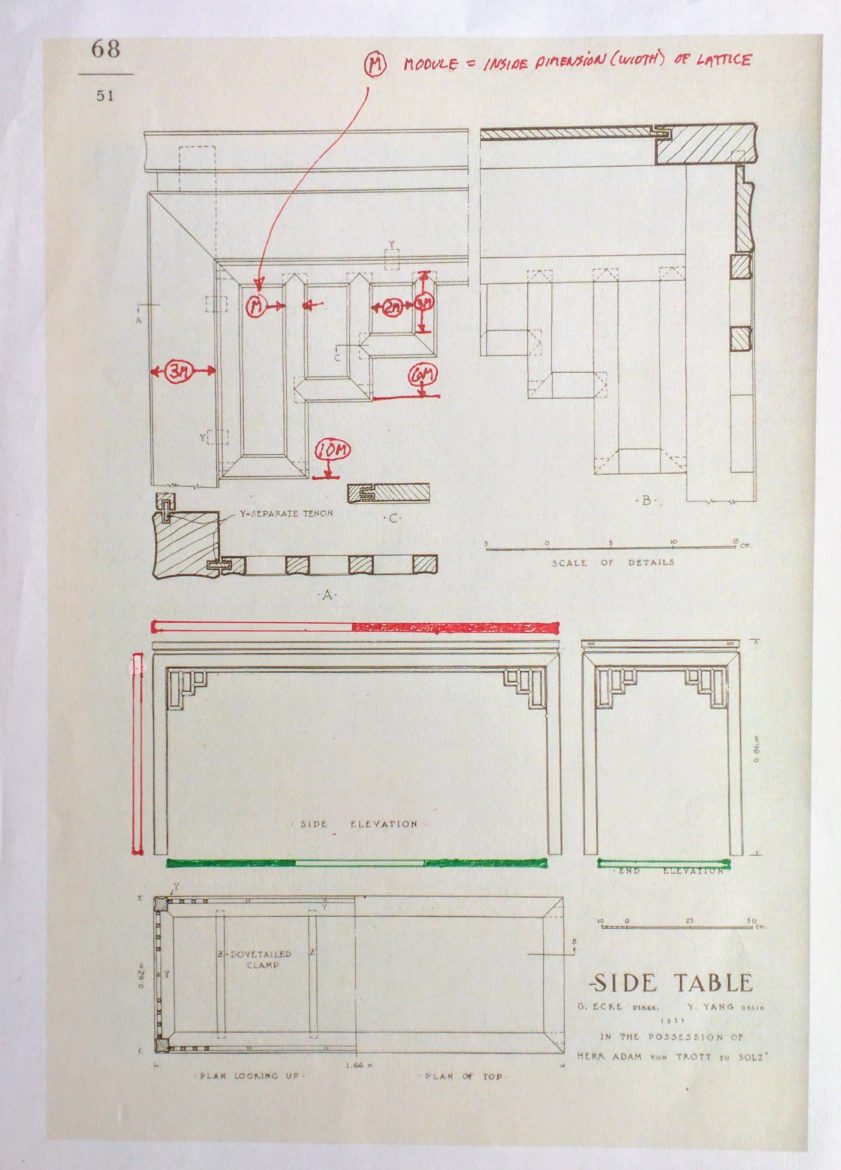
Here’s what the dividers smoke out:
A height-to-length ratio of 1:2
A depth-to-length ratio of 1:3
A lattice design based on a module the size of the batten width resulting in a sequence of ratios 1:1; 2:3 and 3:5 (octave, fifth and sixth musical consonants)
The width of the legs and apron pieces are 3 modules wide
So does East meet West? I believe the dividers would say yes. But they don’t say who influenced who or whether this ancient design method arose independently.
]]>It’s natural to gaze with wonder at a blazing sunset or a beautiful painting. A brilliant idea on the other hand is altogether different. It can slap me in the face and I can step right over it and not see the beauty and possibility laid out before me. Perhaps it’s because the most beautiful ideas are simple. Like the fact that just three primary colors – red, blue, and yellow can combine to make every color imaginable. The simplicity camouflages the deep potential just below the surface.
Until recently geometry was one of those blazing ideas that I just couldn’t see. In the seventh grade it was just a class that required memorizing rules with funny names. Why did they name them after some guy named Pythagoras? No time for deeper questions, just learn the theorems and click them into place to pass a test. No thought that geometry lay at the root behind everything in the built world. No mention that geometry was the key to bring order out of chaos with a few simple lines and a curve or two.
I’m still stepping over the simple and missing the profound. But every once in a while I find a nugget and pause to stop and wonder.
George R. Walker
