
Ouch!
So how do you go about evenly spacing out the slats on a design such as a headboard (as the example shown here by (and I’m not making this up) Funky Chunky Furniture.) Well the oh-so-last-century way to do it (we are talking the 20th) would be to get out our tape measure, take some dimensions and employ a round of algebra to solve the problem. Let’s assume we picked up some 1X6 stock from the lumber yard and measured it out at 5 5/16th inches–or 5.4375 to make it easier on the calculator. We.. also measured the distance between the bedposts (after removing the chewing gum from last night) and came up with 35 15/16th inches or 35.9375. Here’s the Persian’s Al-Jabr solution that we all learned how to do back in High School:
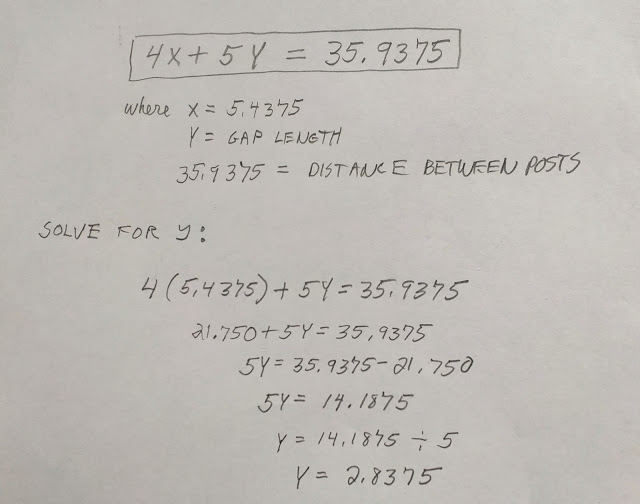
We would then proceed by cleaning the dust of our glasses and measuring out the gap distance of 2.8375 (about 2 13/16) and making a mark, then adding another 5.4375 (5 7/16) and so on. If we’re uncharacteristically careful we’ll get it laid out to within plus or minus about 5/16th (accounting for rounding). Which means we will have to repeat the process a few times to get the layout within a visually acceptable tolerance.
Bring on the Geometry!
If, however, you are familiar with our By Hand and Eye approach to such things, you already know that we can rewind about 20 centuries and do it the way an artisan in the age of Euclid would have gone about it. (We can forget the tape measure–and the eyeglasses–because neither have been invented yet). I probably won’t have to tell you that we’ll come up with the layout more quickly and with far greater accuracy–within .005 inch if our dividers are freshly sharpened (you do sharpen your dividers don’t you?):
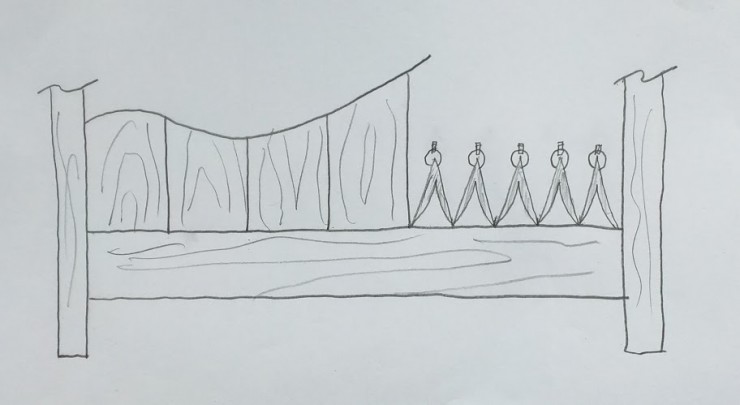
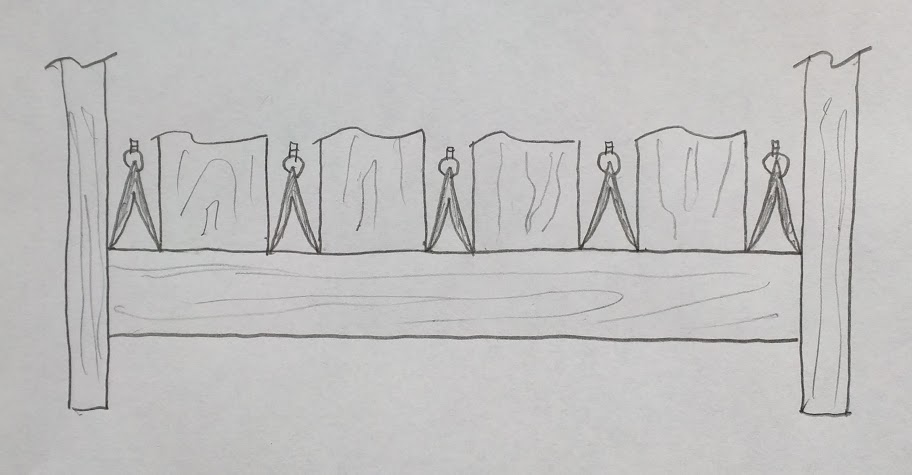
We’ll start by setting the four slats on the rail as shown (for illustration purposes–in actuality we’d likely work with a story stick marked with the span). We then step out five segments in the remaining space. Each segment is the gap between the slats.
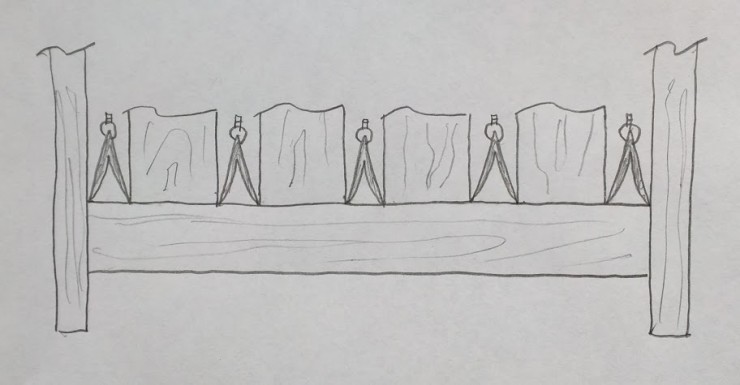
If we are really working in the pre-industrial age/pre-home depot mode, we won’t use an off-the-shelf 1 x 6 for the slats. Instead, we’ll think about the layout as a rhythmic pattern of whole number segments. For example, 2:3:2 repeated:
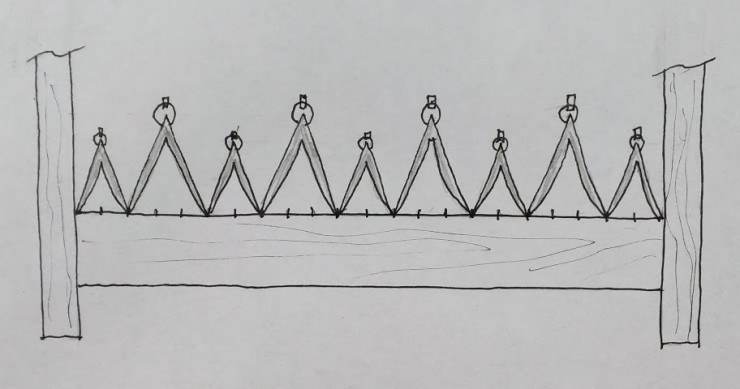
To pull off this feat, we would simply break up the distance between the two posts into however many segments we need to “keep the beat” for four slats. In this example that number would be twenty-two. While it might seem like a lot of work to divide a space equally into this many parts by stepping along with dividers, there are some traditional shortcuts to be had. For example, we could just step off eleven spaces, then find the midpoint of one segment and step off the midpoints of the rest of the segments from there. Another shortcut would be to use a sector–which is exactly what the artisans would do by the time the Renaissance era rolled in. If you’ve read either of our books, you already know all about the sector. If not, you will after you read a post coming soon in this space!
Jim Tolpin



7 thoughts on “Algebra vs. Geometry Smackdown”
nick
Thank you!
Boon
I find myself using these techniques at every available opportunity. I’ve got pairs of dividers stashed everywhere, it now seems subconscious. It is also serious fun. The looks I get from workmates is priceless. Thanks guys.
Jack Ervin
Not being picky just saying ⁵⁄₁₆ is .3215, ⁷⁄₁₆ is .4375. That’s why numbers get in the way isn’t it.
Thanks for this new old way of layout.
Xavi Molina
wow!! Very useful!! 1000 thanks
Rusty
Why not lay in the slats diagonally and parallel to one another, making sure the first slat contacts the headboard and side board while the last slat contacts the foot board and opposite side board? Measure the distance between the corner on any slat and the respective corner on an adjacent slat. This is the measurement of slat and gap combined. Of course, this produces 1 less gap than the number of slats provided with the bonus being the extreme corners of your mattress or box spring are now supported in exchange for an increase in gap to about 4 and 11/16 inches (4x + 3y).
taraine
Is there an ‘easy’ way to ‘step it out’ with dividers? Is it just trial and error until you get exactly 5 (or whatever) steps? Perhaps, as I am a child of the decimal and derivative math systems, I am incapable of seeing the obvious, but I have no idea how to actually use dividers to do anything useful. The idea is grand, but I need practical help.
Thanks.
Jim Tolpin
Taraine: Check out the other posts in this blog about using the sector and dividers. With just a little study you’ll see how incredibly useful, not to mention easy, these methods are. Of course, the books we wrote on the subject go into these techniques in excruciating detail and we would be remiss not to shameless encourage you to check them out as well!