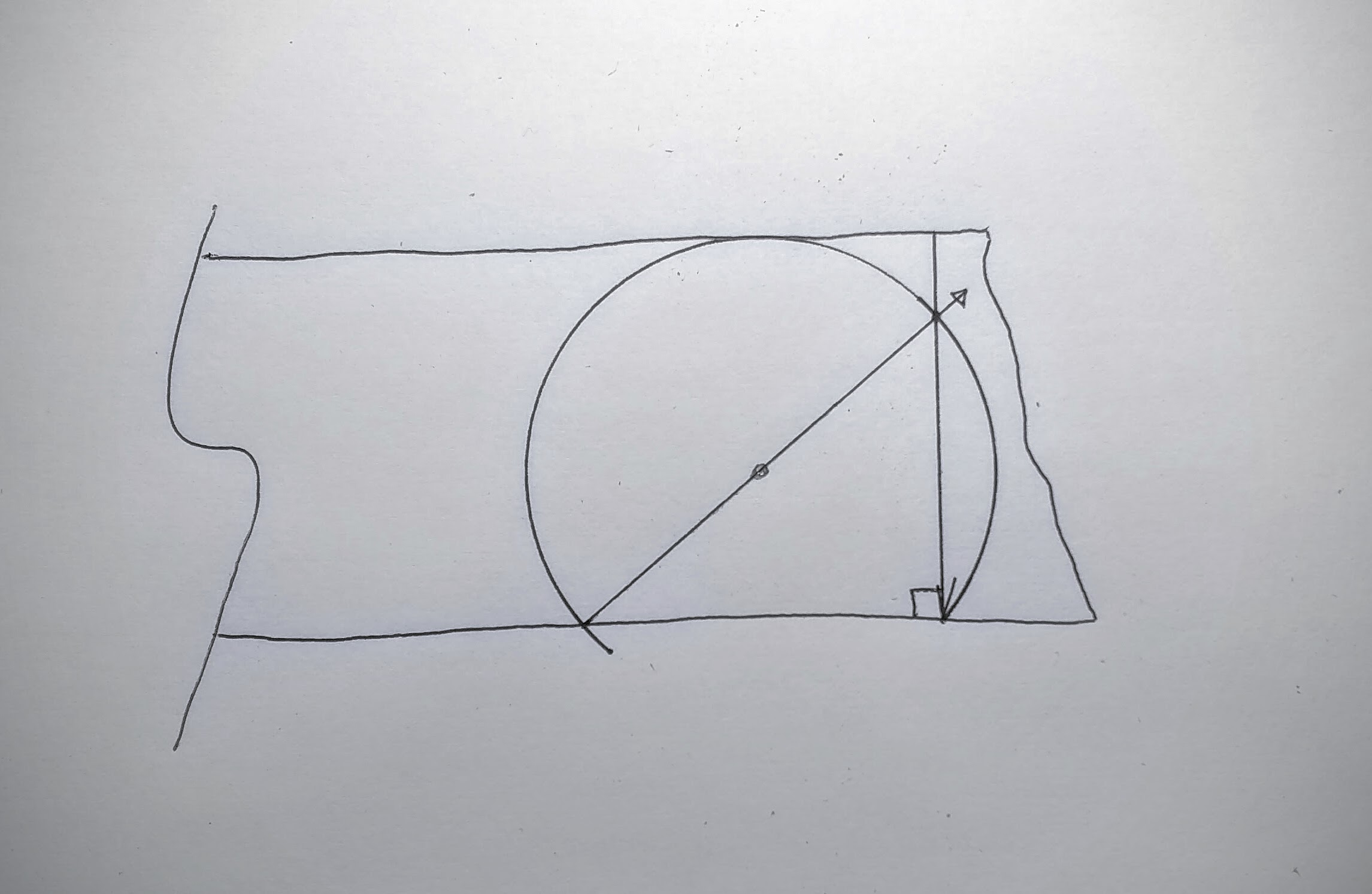
The following sequence of steps show how to use simple geometry to create a right angle along the edge of a board–demonstrating that you don’t need a square to make a square layout line. Handy if you are making a square clamping jig to clamp the blade and tongue of a square together so you never have to do this again! The resulting try square is essentially a template of a right angle.
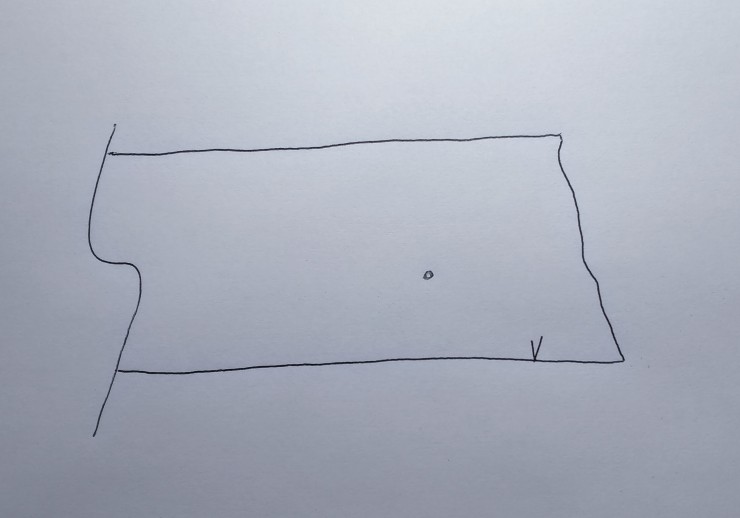
Put a mark on the edge of the board where you want to construct the right angle crosscut.
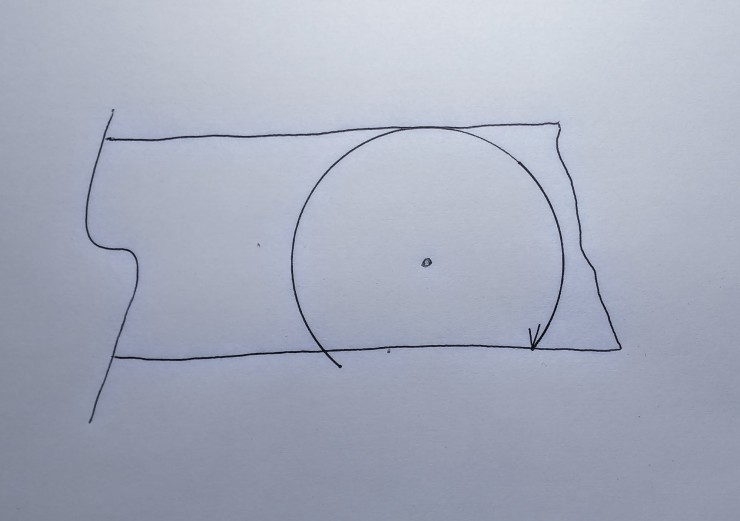
Locate the focal point of a circle that will pass through the starting mark. The circle must be sized to fit on the board as shown above.
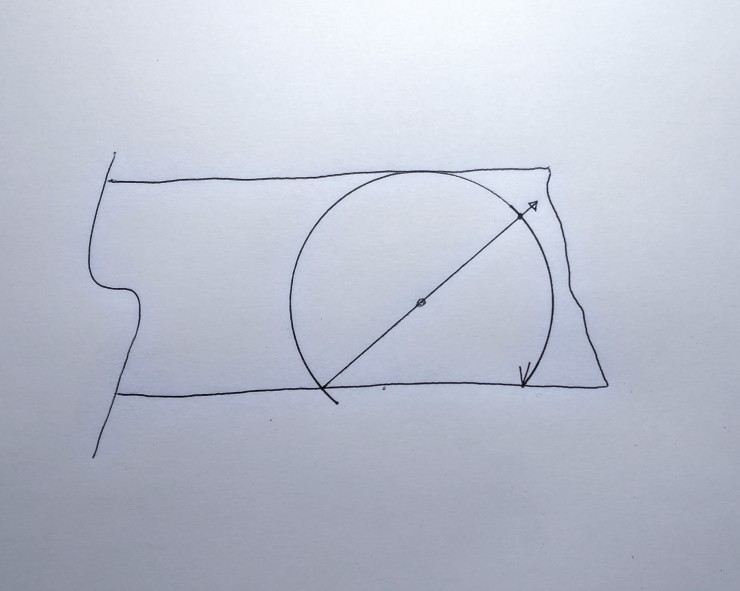
Draw a diameter line as shown from the edge of the board intersection through the focal point.
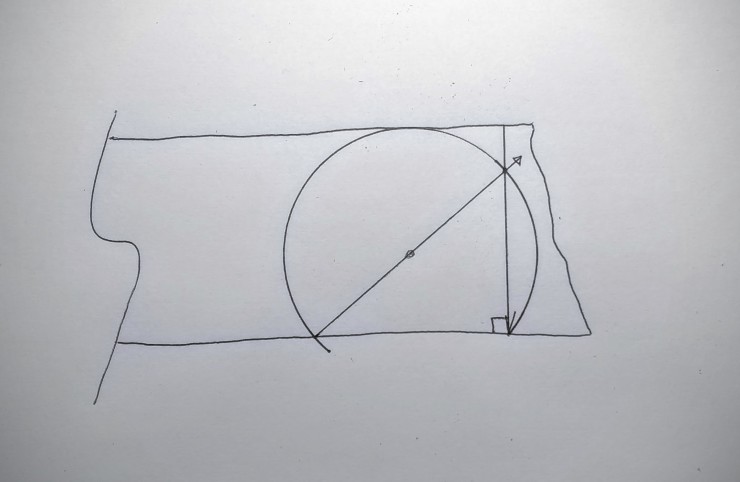
Draw a line from the V mark through the point where the diameter line passes through the rim of the circle. This line will be square to the boards edge as predicted by Thales theorem.



11 thoughts on “Be There AND Be Square!”
jbaker4041
Sorry, don’t get it. Wait! I do… Wow. So simple to do. It is something about two triangles sharing an apex and the same length legs. I’d love to see the geometric proof.
magman07
Could you define the steps you took, please?
Jim Tolpin
I added some captions to the drawings…hope that helps.
magman07
Thank you that helps, I have a definite learning process until some point it just leaps out at me.
jbaker4041
Draw a diameter and any radius. connect the end of the radius and to the ends of the diameter to produce two triangles. X and y are the angles at the center of the circle. a and b are the opposing angles (two of each).
1) The sum of the apex angles (x and y) of the two triangles equals 180 degrees (since diameter is straight line).
2) The two triangles are isosceles, with legs equal to the radius, so each triangle’s opposing angles (a and b) are equal.
3) Sum of apex and opposing angles of each triangle is 180 degrees. So sum of two triangles is 360 degrees.
4) Bases meet at angle equal to sum of one opposing angle from each triangle. Math is:
X + 2a + Y + 2b = 360 subtract x+y = 180
2a + 2b = 180 divide by 2
a + b = 90
Jim Tolpin
The construction is from Thales’ theorem which basically shows rim shots from a diagonal always produce a right angle.
taraine
Perhaps this goes without, but this presumes that the sides of your board are parallel. If you haven’t planed the second side, or you are trying to find a right angle on an irregular form, this won’t suffice.
Jim Tolpin
The only straight line you need to start out with is the edge of the board to which you are going to draw the right angle. The opposite edge is of no consequence.
marphlix
Does the circle need to touch the top side of the board, or can the circle be smaller than the height of the board, provided it crosses the bottom?
I hope that makes sense
marphlix
Nevermind, i just re-read your description and think i worked it out
Jim Tolpin
You got it…it just has to cross over the bottom.