Well no, dear, the curvaceous tapering just makes you look muscular. Or maybe it’s just an optical illusion. Or maybe the builders knew that the swelling, though slight, imparted a bit more strength to the column. But let’s not get hyperbolic and go too far on these theories. It’s good to leave a little out (speaking elliptically) so let’s step away from this parabolic trajectory of conjecture and look at the types of tapering that can be generated with simple geometric constructions.
In our book By Hand and Eye, we showed a simple straight taper–common enough in Roman columns and quite easy to generate. But some columns from Greek antiquity display a taper that follow a curve. As shown in the drawing below, the curves get more radical as you move from parabolic to elliptical to hyperbolic. All were developed, not from a numerically dimensioned layout, but from the generation of a relatively simple geometric construction familiar to ancient artisans.
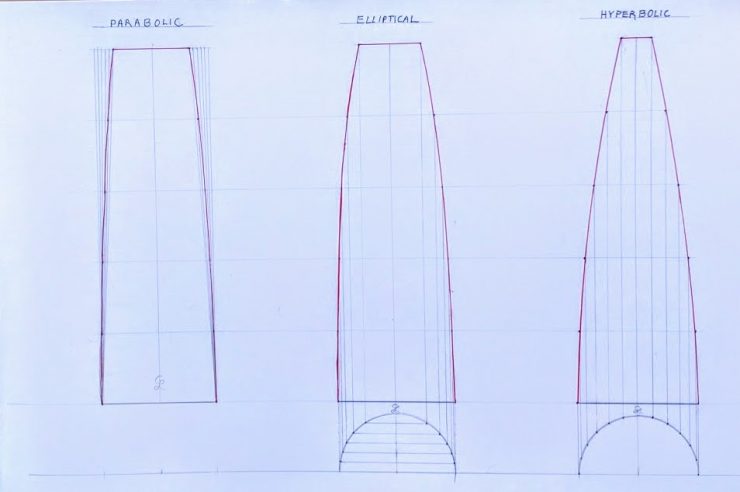
The parabolic curve is the simplest and fastest to execute. As shown in the drawing, it is simply a matter of dividing up (with dividers of course) the inset amount of the top of the column into equal segments, than running straight lines (with a straightedge or string) from these points to the corner of the column shaft at the base. You then create station points at evenly spaced, horizontal intervals drawn across the length of the column. (I show only four intervals here for clarity–plus I’ve compressed the height-to-width ratio to exaggerate the curve).
To create the elliptical curve, the artisan drew a half circle to the diameter of the bottom of the shaft, then segmented the half sector into six even slices. Lines drawn vertically from the intersection of the horizontal segments with the rim of the arc create your station points above.
The hyperbolic curve station points arise from evenly spaced segments stepped along the circumference of the half circle.




2 thoughts on “Does this Entasis Make Me Look Fat?”
Cathy
Entasis comes from the Greek word meaning “strain”. Speaks toward the entasis having something to do with resisting a force.
Jim Tolpin
Exactly!