Say you have a bunch of logs that you want to turn into beams…big beams…beams so big that you basically want to turn the round log into the largest rectilinear cross-section beam you can get out of it. So where do you turn to find the most efficient way to layout the cross section on the end of the log? To Thales of course…and to old timber framers, rules of thumb. First, though, you must decide whether you want to get the strongest beam possible, or the stiffest beam possible. Follow along as we work out the latter using Thales Theorem of creating right angles–and ultimately rectangles–within a circle:

First, draw the largest circle you can on the end of the log.
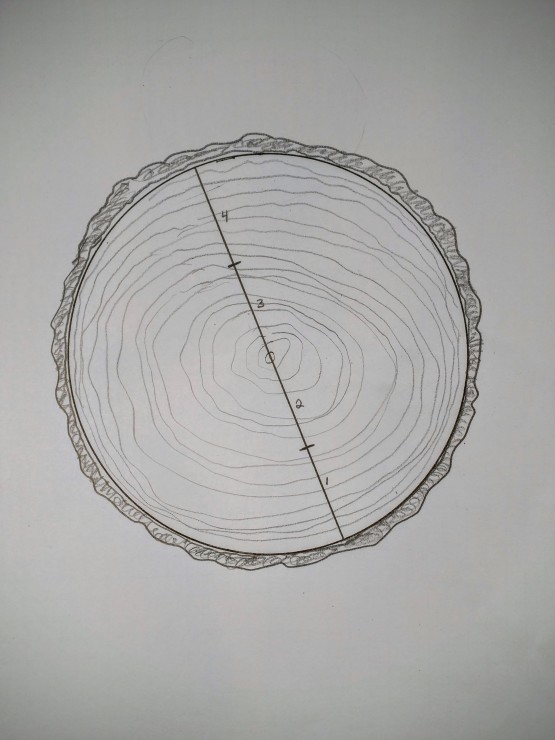
Next, draw a diameter line through the focus and break the line up into four equal segments (step it out with dividers so you don’t have to screw around with dividing fractions.)
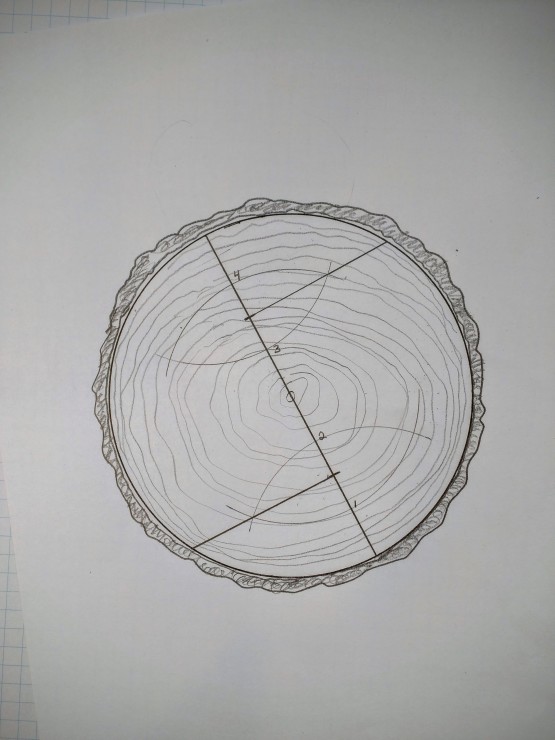
Erect a line at a right angle from the first and third segment points (using geometry and a scribing compass of course), extend them to touch the circle. Here’s where Thales comes in:
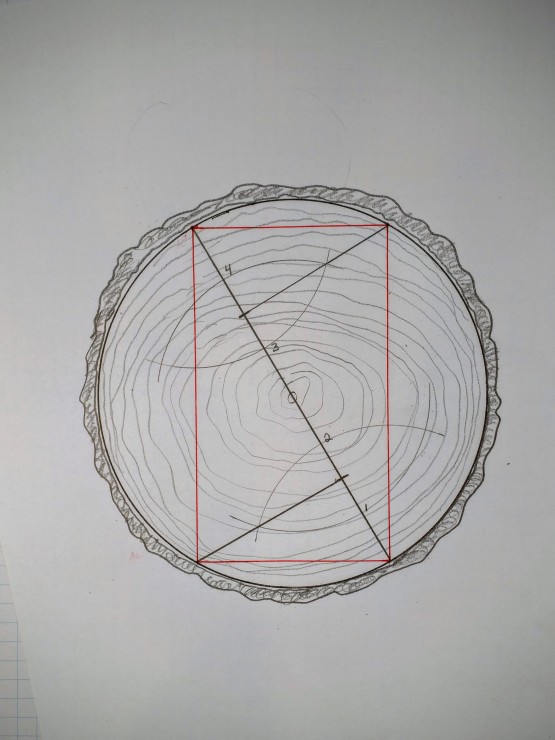
Connect the ends of the diameter line to the two intersection points you just created. The angles here will be right angles and the resulting form is a rectangle. In this case the largest rectangle that produces the stiffest beam. If you want the strongest possible beam, the rule of thumb is to break the diameter line into three (instead of four) segments and create the rectangle as shown below:
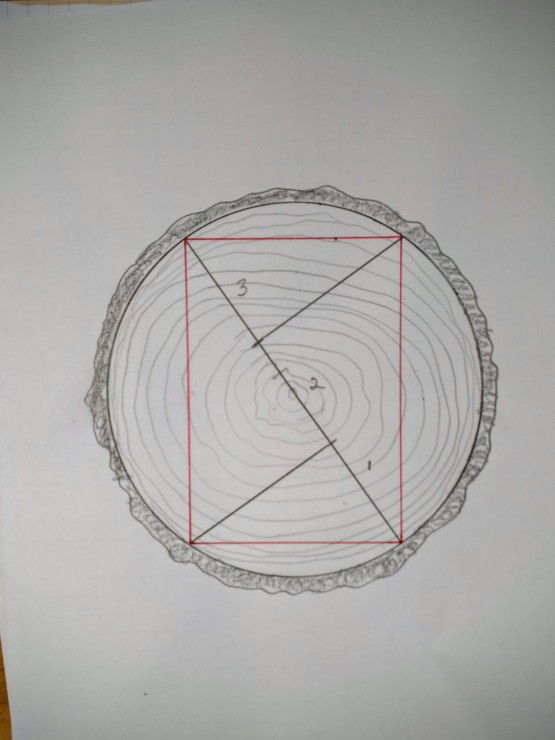
Your welcome.




2 thoughts on “More Thales”
John Holchin
Is there an approximate age for those rules of thumb? I’m interested in how far it predates the engineering theory.
Euler-Bernoulli beam theory describes beam deflection and stress and was first defined around 1750, but significant application didn’t happen for about another 100 years. The stiffness comes down to the second moment of area (b*h^3)/12. The strength comes down to section modulus (b*h^2)/6. When I played with the numbers, the base of the stiffest beam is about 50% of the diameter of the log and the base of the strongest beam is about 60% of the diameter of the log. The pictures on the screen match this well.
Jim Tolpin
John: As George mentioned in a recent post, the knowledge of plane geometry goes back well before recorded history as is made evident in excavations of constructions in Turkey dating back at least 9000 years. I doubt anyone could place an exact date or person behind these probably empirically-derived rules of thumb for beam size. If you have any ideas about their origins, I’d love to know about it. George found these drawings in a late 19th century text.