Geometry is a mysterious bird. The ancient geometers thought it mysterious because its secrets were like jewels that fell from the heavens. Though it’s the earliest form of mathematics, it doesn’t rely on numbers. In its purest form, geometry was expressed using points, lines, and elemental shapes such as the circle and the square to prove a geometric truth.

On a practical level, builders used geometry to determine if something is true. In other words, is that wall plumb, is that foundation level etc. That’s a far cry from today, where everything is described with numbers from your shoe size to the calories on that bag of chips you shouldn’t be eating.
Our new book “Euclid’s Door”, describes how to build a kit of layout tools and in the process unlock the hidden geometry. Early on, we were curious to explore just how true we could make these tools using hand methods and the power of geometry. I confess, I reached into my machinist tools to quantify the results of our efforts. That became a big “aha” moment. We discovered we could indeed make wooden tools that stand up well and even exceed their modern metal cousins. How could this be possible?
Here’s a simple but important principle. If you magnify the distance of the thing you are trying to measure, it increases your ability to gauge with precision. Using winding sticks is a good example of this in action.
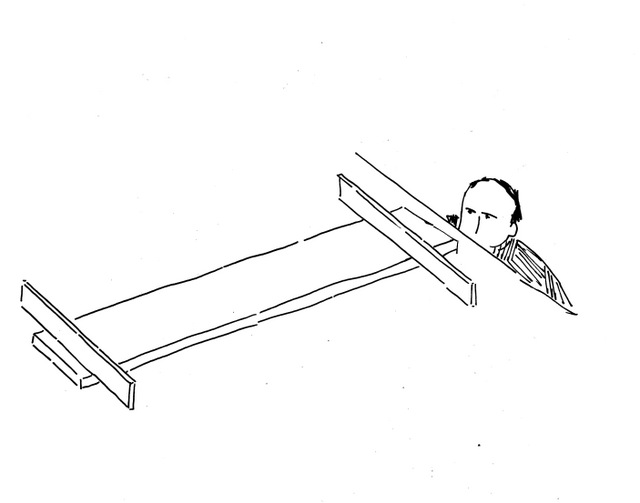
The length of the sticks exaggerate the width of the board to magnify any twist. Another example is to draw two parallel lines. You can prove they are indeed parallel if you extend the lines out and they never cross. For our purposes on the tool builds we found we could achieve magnificent results extending lines out with our three foot long wooden straight edge. We used this principle to work out a simple proof for every tool.
Here’s a couple of other examples of that principle that illustrates the power of it. Take a machinist’s micrometer. It’s really just a screw that has a scale we can read to help us measure with precision. Yet it is able to perform at a high level because it mechanically exaggerates the distance of what it’s measuring. One turn of the thimble (the part that has the scale on it) advances the plunger (the part that touches the work) 0.025”. It takes forty revolutions to advance the plunger one inch.

Yet in those forty turns, the thimble travels round and round the barrel of the micrometer and in reality it travels a distance of about six inches. So the travel ratio is about 6:1. Another good example is a tall case clock. It uses weights to drive the hands, but the precision is controlled by the motion of a pendulum. In one hour, the tip of the minute hand on a dial traces a circle that’s a bit over 30 inches in circumference. In that same hour the pendulum below swings out the beat of 3,600 seconds.

In that same space of one hour, that pendulum travels over half a mile. Most clocks have a screw mechanism to raise or lower the pendulum bob. In this way, the pendulum swing can be altered slightly. This allows the clock to be adjusted with great precision.
Humor me and let me take you down a rabbit hole. Most of the things we typically measure are expressed with a number i.e. inches, pounds, minutes, etc. These measurements that are expressed as a number all require a “master” or standard. In my former life in industry we kept and maintained masters that we used to make sure the tools and product were correct. These masters were all checked ultimately against a set of “Grand Masters’ in a vault. Those Grand Masters were sent to the Bureau of Standards in Washington D.C. once a year to verify they were correct.

Not sure what the technology is today, but even back in the 1970’s, the D. C. lab checked our Grand masters against a beam of light with a wavelength that defined ground zero. In the case of measuring time, early clock makers had to turn to the heavens for a suitable time master. Note, they were looking to something at great distances to get their master time. Every major seaport across the globe went to great expense to set up and maintain a master clock that naval navigators could set their timepieces to. In both these cases the process of developing and improving a master to support the entire enterprise required tremendous resources.
Compare that to this simple geometry our ancestors discovered. It doesn’t use numbers to measure but instead uses lines to verify if something is true i.e. are the lines parallel or do they intersect in the right spot. It put tremendous power into the hands of ancient builders that only required a few bits of string and a couple of straight sticks (which are self proving). Put that in your pipe and smoke it.




2 thoughts on “Numbers Versus True”
bobeaston
“Euclid’s Door” has been an excellent guide for me. Your techniques have helped me prove some of my earlier built tools and are helping create newer, better, versions of others. THANKS for this great learning tool.
Bob Easton
George Walker
Glad to hear that. Yes the ideas have a broader application. Nice to see you find it helpful.