Old School Framing Square Trick #1

One of the primary uses of the framing square is to create slope lines for calculating unknowns–not necessarily in all cases to high precision, but to get you well within the ballpark. In this example shown in the photo above I created a pair of slope lines to determine the conversion between metric and imperial measurements.

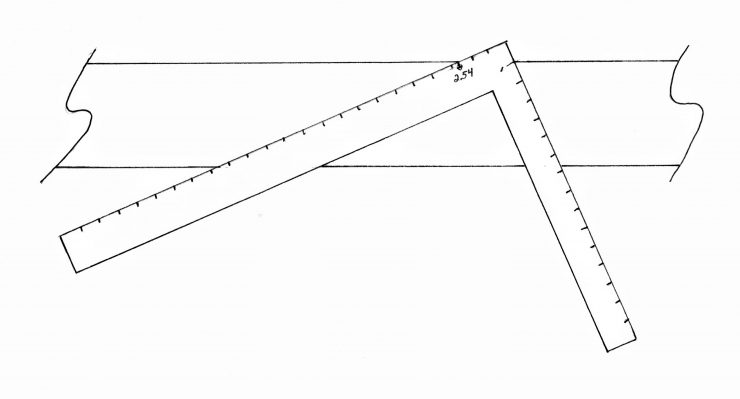
To set up the lines, you start by getting out a piece of wood with a nice straight edge, then orient the square to this edge so you can draw the slopes across the face of the board for “slipping” the square. Set up the ratio between the two legs in which the root number is one while the other number is the proportional relationship you desire. In this case, since we want to convert centimeters to inches (or vice versa) we want a ratio of 2.54 to 1 (I looked that up in a book–you could simply hold a metric to an imperial rule together!). Now orient one leg so the 1.00 mark touches the edge; orient the other so 2.54 (about 2 9/16) touches. Draw slope lines to both legs so you can convert either way.

In the photo above, I’ve set up the square to convert inches to centimeters. Along the inches slope line I’ve slipped the square until 2.25-inches comes to the edge of the board. I then read the number on the other leg: about 5.75 cm.

In this example I’m asking how many inches equal 4 centimeters. So I slip the left hand leg on the centimeter slope line until I read 4.o centimeters at the edge. On the opposite leg I then read (about) 1 5/8 inches. Again, these are ball park (within 1/16-in.) figures. If you need more accuracy, you can always consult the table hiding somewhere on your bookshelf or bring up the conversion calculator online. Doing it this old school way, if nothing else, cements the idea of using the framing square to determine proportional relationships via ratios. Of that, we will have much more to say down the road.