Amongst this collection of Masonic “Past-Master’s Jewels” medals, two show a representation of the pythagorean theorem. It is reported that its presence on the owner’s medal indicates that person was what we would likely now call a crew foreman. Once of his many responsibilities was to ensure that all the layout tools were true–a clue to why the homage to Pythagoras. This theorem, codified later by Euclid into his “Proposition 47”, offers a logic proof that the area of the squares erected on the legs of a right triangle would equal the area of the square erected on its hypotenuse. That’s all well and good, but why would that particular equation be of vital interest to the foreman of a joiner’s or mason’s crew? To try to find out, I decided to construct an exact-as-possible, large-scale drawing of the graphic upon which I could explore with a pair of dividers.
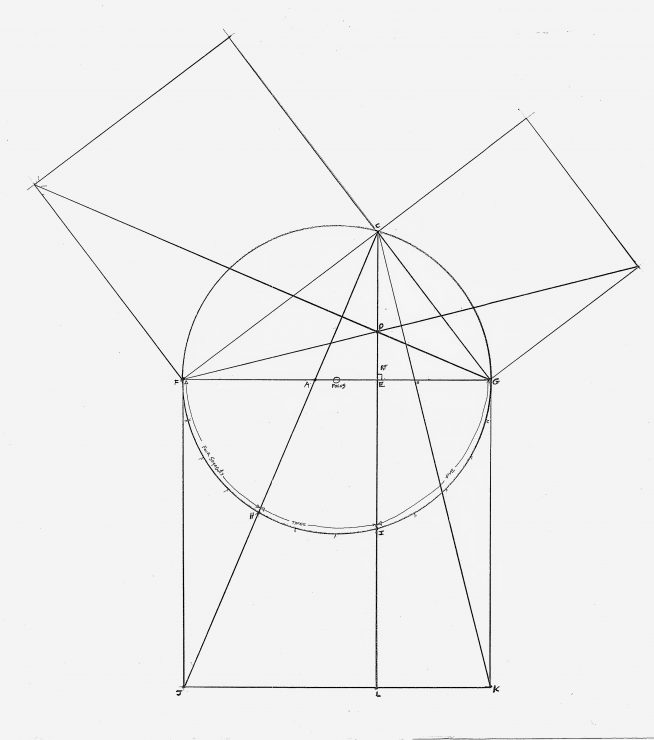
The first thing I discovered was that the vertical line CL, which is fixed by the inherent base line’s intersection points C and D, forms a right angle with the hypotenuse. Even though this result is likely nothing more than symbolic (there are a lot easier ways to generate a right angle with a compass and a straightedge), I believe this right angle–hidden in plain sight–is probably as important to the metal (and its wearer) as the theorem itself. The right angle (“recto” in Greek) is simply the right way to set a vertical post. (Wood’s superb resistance to compression happens when, and only when, the post is set at a right angle to level–an orientation that aligns the grain parallel to the force of gravity). It’s also the right angle to create symmetry to a baseline in common rectilinear structures (think cathedrals).
No reason to stop there, though. Exploring further revealed other attributes to this graphic that offer additional symbolic (and real) representations of the truths inherent in Geometry (note the traditional capital G). Print out the template (you’ll find it on the shopping page of this site) and take a look around on it for yourself. You’ll discover triangles with perfect 2:3 base-to-height proportions (one of the fundamental harmonics in music and architecture of the medieval era); you’ll find sequences of the infamous triplet (the 3-4-5 triangle) revealed in the hypotenuse and even in the circumference of the circle that started it all; and you may find the module upon which the entire construction revolves. Have fun with this–I sure did!
By the way: If you want to buy the medal shown, you can find it here



