The Power of Geo-Metron

Or what we call earth-measure today: Geometry. This was man’s most ancient field of study leading to an understanding of the primary structure–dare we say truth–of the patterns underlying all of nature. An understanding which could be parsed, and demonstrated, with two simple tools: A single stick (i.e. a straightedge) and a hinged pair of sticks (i.e. a compass/divider).

This guy, Eratosthenes (the chief librarian at the Library of Alexandria), used these two tools to measure the circumference of the earth more than 200 years BCE. And he got it right within less than one percent of error according to some documents.

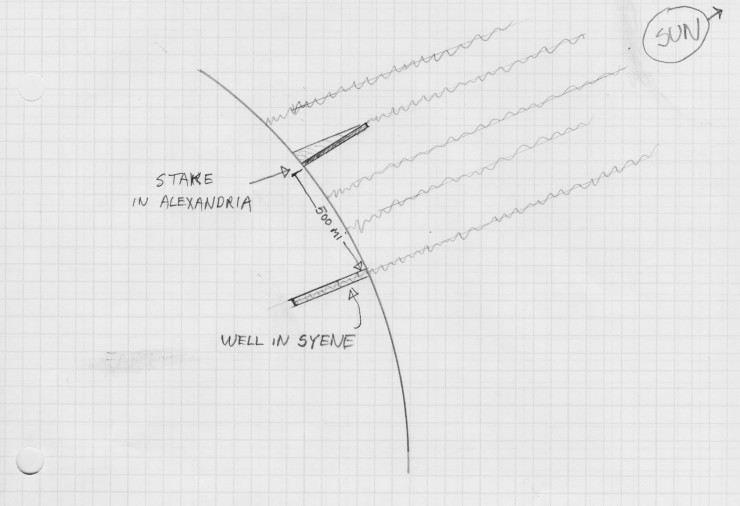
So how did he do it? He used observation and the principles developed by Euclid a generation earlier. The observation part: First, he knew (as did his contemporaries) through simple observations that they were living on a sphere, not a flat plane. (A fact somehow lost on some Northern Europeans in the 19th century). He also observed that the sun on solstice day at noon in Syene (which lay exactly 500 miles due south of Alexandria) shined directly down the shaft of a well. He also noted that posts erected plumb cast no shadow at that time and place. On that same day, he had observed no such thing in Alexandria: wells stayed dark and upright posts cast shadows.

A map of the western world from the time of Eratosthenes

To calculate the circumference of the sphere that he knew was causing this effect, the librarian/geometer drove a stake in the ground at Alexandria, plumbing it true with a weighted string. (Essentially creating a “gnomen”–the working part of a sundial). At high noon he lifted the length of the shadow using a pair of dividers. The span of the dividers now represented the 500 mile length of the arc between the stick and the well in Syene–at a reduced scale of course.

How did Eratosthenes know the distance between the cities you ask? By reading the existent maps already in use in Egypt whose and land measurements were carefully calculated by lots of guys walking or riding camels in straight lines and stretching out long ropes behind them. Really.

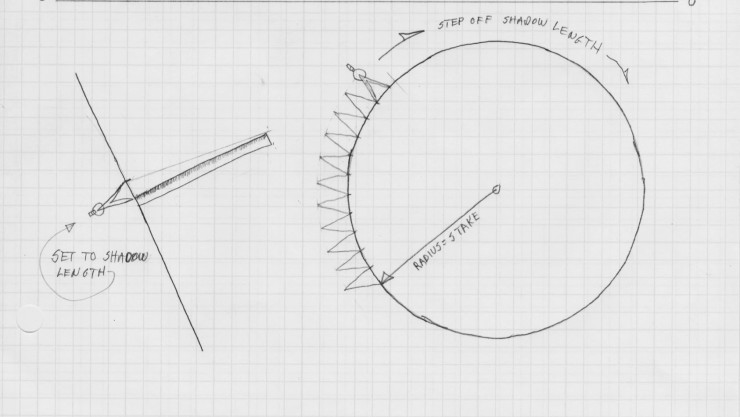
To get the circumference of the earth, he first created a circumference to scale from the stake–a simple matter of using the length of the stick as the radius of the circle. He then used the dividers (at its scale of 500 miles) to step around the scaled-down earth. He came up with forty nine steps plus most of the fiftieth. Since fifty of the five-hundred increments counts up to 25,000, he knew the earth’s diameter must be just under that number. Parceling out the last step to smaller segments, he came very close to the actual number of 24, 901 miles (of course back then he was working in “stadia” as a unit of length.) No matter what you read on the internet, he didn’t use degrees to make the calculation–the mathematics of degrees and decimal numbers in general hadn’t been invented yet–and wouldn’t be for more than a millennium.)

The Geometry Behind the Calculation:

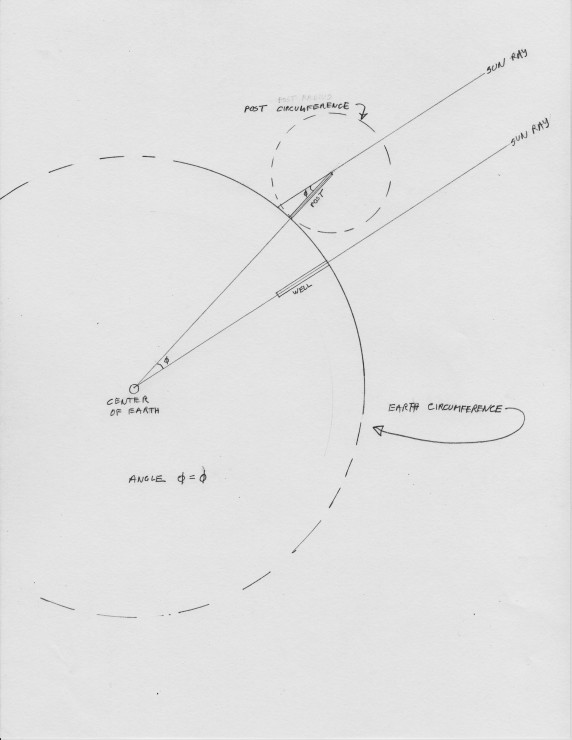
Since the sun’s rays are (for all practical purposes here on earth) parallel, we can represent them as parallel lines. One line goes down the well to the center of the earth–which is also the focal point of the circle representing the earth. The second line clips the top of the post and casts a shadow of a certain length on the ground. If you draw a line down the center of the post to the center of the earth, the angles formed have to be the same (as explained by Eratosthene’s colleague Euclid). This gives you a simple equivalency: the distance between the post and the well is described by the same angle (or sector of a circle) as the angle producing the shadow distance. Therefore, both distances are the same sector of a circle: here about one fiftieth.

Jim Tolpin