If you think back to your days in what used to be called “Grammar School”, you may remember old Mr. Hammersmacker (or was it Miss Hellena Handbasket?) droning on about the Pythagorean Triplet and how that was somehow related to taking the square root of something you just squared to come up with something called a “proof”. Of what you probably don’t remember because as soon as they said “triplet” you were thinking how cute that set of triplets was in the grade ahead of you. And they weren’t square either.
Anyway, I digress. The triplet is simply a sequence of straight line lengths that, when tied together, will form a right angle in one of the corners. Specifically, if the ratio of the lengths is in exact 3:4:5 (or 6:8:10 etc.) segmented increments, the right angle forms at the intersection of the 3 and 4 segment lines. This sketch shows you how an artisan could prove this with a simple construction (as opposed to an algebraic proof):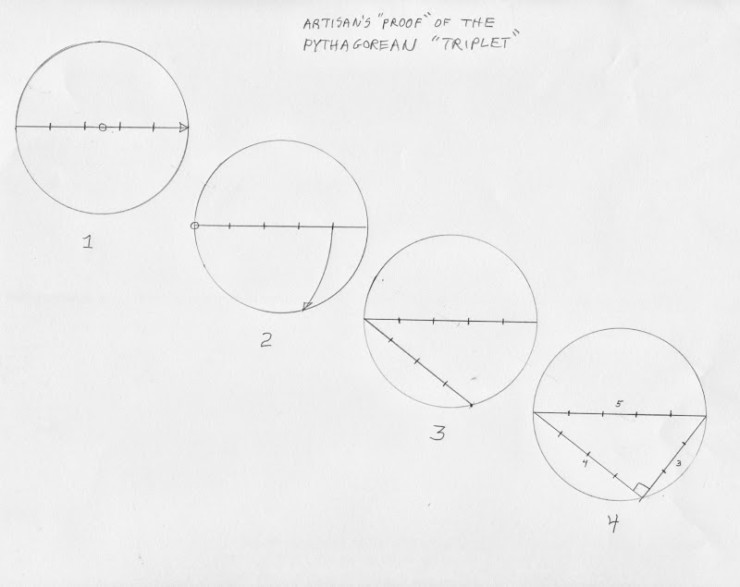
Step 1: Draw a diameter line (i.e. any line through the focal point). Divide it into five parts. (Use a geometric construction, a sector, or just step and tweak).
Step 2: Set the compass from the rim intersection point to the fourth segment mark.
Step 3: Swing an arc down to intersect the rim. Draw a line to this point. This line is four segments long.
Step 4: Draw a line from this intersection point to the other diameter rim intersection point.
Step 5: Set the dividers to the segment length and step out along the length of this last line. You will find it to be exactly three segments long, proving the truth of the 3-4-5 triplet.
In a following post, as soon as I can stop thinking about Joyce, Judy and Jane (I’m not making this up, by the way) I’ll show you how artisans used this geometric truth to create tools that allowed them to quickly and accurately lay out a right angle, from the small scale needs of a furniture maker to the large scale work of a cathedral builder. First though, I think we should address that burning question you’re just dying to ask: “Did you ever get a date with one (or more) of the triplets?” No that’s not the question (and if it was the answer is no, at least not yet). This is the question: “What makes the right angle a right angle anyway?”
Jim Tolpin